Advertisements
01
路程問題(相遇)
【口訣】:
相遇那一刻,路程全走過。
除以速度和,就把時間得。
舉例: 甲乙兩人從相距120千米的兩地相向而行,甲的速度為40千米/小時,乙的速度為20千米/小時,多少時間相遇?
相遇那一刻,路程全走過。即甲乙走過的路程和恰好是兩地的距離120千米。
除以速度和,就把時間得。即甲乙兩人的總速度為兩人的速度之和40+20=60(千米/小時),所以相遇的時間就為120÷60=2(小時)
02
路程問題(追及)
【口訣】:
慢鳥要先飛,快的隨后追。
先走的路程,除以速度差,時間就求對。
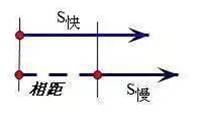
舉例:姐弟二人從家里去鎮上,姐姐步行速度為3千米/小時,先走2小時后,弟弟騎自行車出發速度6千米/小時,幾時追上?
先走的路程,為3×2=6(千米)
速度的差,為6-3=3(千米/小時)。所以追上的時間為:6÷3=2(小時)
03
雞兔同籠問題
【口訣】:
假設全是雞,假設全是兔。
多了幾只腳,少了幾只足?
除以腳的差,便是雞兔數。
舉例:雞免同籠,有頭36 ,有腳120,求雞兔數。
求兔時,假設全是雞,則免子數=(120-36×2)÷(4-2)=24
求雞時,假設全是兔,則雞數 =(4×36-120)÷(4-2)=12
04
和差問題
已知兩數的和與差,求這兩個數。
【口訣】:
和加上差,越加越大;
除以2,便是大的;
和減去差,越減越小;
除以2,便是小的。
舉例: 已知兩數和是10,差是2,求這兩個數。
按口訣,大數=(10+2)÷2=6,小數=(10-2)÷2=4
05
濃度問題(加水稀釋)
【口訣】:
加水先求糖,糖完求糖水。
糖水減糖水,便是加水量。
舉例: 有20千克濃度為15%的糖水,加水多少千克后,濃度變為10%?
加水先求糖,原來含糖為:20×15%=3(千克)
糖完求糖水,含3千克糖在10%濃度下應有多少糖水,3÷10%=30(千克)
糖水減糖水,后的糖水量減去原來的糖水量,30-20=10(千克)
06
濃度問題(加糖濃化)
【口訣】:
加糖先求水,水完求糖水。
糖水減糖水,求出便解題。
舉例: 有20千克濃度為15%的糖水,加糖多少千克后,濃度變為20%?
加糖先求水,原來含水為:20×(1-15%)=17(千克)
水完求糖水,含17千克水在20%濃度下應有多少糖水,
17÷(1-20%)=21.25(千克)
21.25-20=1.25(千克)
07
和比問題
【口訣】:
我的比你多,倍數是因果。
分子實際差,分母倍數差。
商是一倍的,乘以各自的倍數,兩數便可求得。
舉例: 甲數比乙數大12,甲:乙=7:4,求兩數
先求一倍的量,12÷(7-4)=4,
所以甲數為:4×7=28,乙數為:4×4=16
08
差比問題
【口訣】:
我的比你多,倍數是因果。
分子實際差,分母倍數差。
商是一倍的,乘以各自的倍數,兩數便可求得。
舉例: 甲數比乙數大12,甲:乙=7:4,求兩數
先求一倍的量,12÷(7-4)=4,
所以甲數為:4×7=28,乙數為:4×4=16
09
工程問題
【口訣】:
工程總量設為1,1除以時間就是工作效率。
單獨做時工作效率是自己的,一齊做時工作效率是眾人的效率和。
1減去已經做的便是沒有做的,沒有做的除以工作效率就是結果。
舉例:一項工程,甲單獨做4天完成,乙單獨做6天完成。甲乙同時做2天后,由乙單獨做,幾天完成?
{1-(1÷6+1÷4)×2}÷(1÷6)=1(天)
10
植樹問題
【口訣】:
植樹多少棵,要問路如何?
直的加上1,圓的是結果。
舉例-1:在一條長為120米的馬路上植樹,間距為4米,植樹多少棵?
路是直的。所以植樹120÷4+1=31(棵)
舉例-2:在一條長為120米的圓形花壇邊植樹,間距為4米,植樹多少棵?
路是圓的,所以植樹120÷4=30(棵)
11
盈虧問題
【口訣】:
全盈全虧,大的減去小的;
一盈一虧,盈虧加在一起。
除以分配的差,結果就是分配的東西或者是人。
舉例-1: 小朋友分桃子,每人10個少9個;每人8個多7個。求有多少小朋友多少桃子?
一盈一虧,則公式為:(9+7)÷(10-8)=8(人),相應桃子為8×10-9=71(個)
舉例-2: 士兵背子彈。每人45發則多680發;每人50發則多200發,多少士兵多少子彈?
全盈問題。大的減去小的,則公式為:(680-200)÷(50-45)=96(人)則子彈為96×50+200=5000(發)
舉例-3: 學生發書。每人10本則差90本;每人8 本則差8本,多少學生多少書?
全虧問題。大的減去小的。則公式為:(90-8)÷(10-8)=41(人),相應書為41×10-90=320(本)
12
牛吃草問題
【口訣】:
每牛每天的吃草量假設是份數1,
A頭B天的吃草量算出是幾?
M頭N天的吃草量又是幾?
大的減去小的,除以二者對應的天數的差值,
結果就是草的生長速率。
原有的草量依此反推。
公式就是A頭B天的吃草量減去B天乘以草的生長速率。
將未知吃草量的牛分為兩個部分:
一小部分先吃新草,個數就是草的比率;
有的草量除以剩余的牛數就將需要的天數求知。
舉例: 整個牧場上草長得一樣密,一樣快。27頭牛6天可以把草吃完;23頭牛9天也可以把草吃完。問21頭多少天把草吃完。
每牛每天的吃草量假設是1,則27頭牛6天的吃草量是27×6=162,23頭牛9天的吃草量是23×9=207;
大的減去小的,207-162=45;二者對應的天數的差值,是9-6=3(天)結果就是草的生長速率。
所以草的生長速率是45÷3=15(牛/天);原有的草量依此反推。
公式就是A頭B天的吃草量減去B天乘以草的生長速率。
所以原有的草量=27×6-6×15=72(牛/天)。
將未知吃草量的牛分為兩個部分:一小部分先吃新草,個數就是草的比率;這就是說將要求的21頭牛分為兩部分,一部分15頭牛吃新生的草;剩下的21-15=6去吃原有的草,所以所求的天數為:原有的草量÷分配剩下的牛=72÷6=12(天)
13
年齡問題
【口訣】:
歲差不會變,同時相加減。
歲數一改變,倍數也改變。
抓住這三點,一切都簡單。
舉例-1: 小軍今年8 歲,爸爸今年34歲,幾年后,爸爸的年齡的小軍的3倍?
歲差不會變,今年的歲數差點34-8=26,到幾年后仍然不會變。
已知差及倍數,轉化為差比問題。26÷(3-1)=13,幾年后爸爸的年齡是13×3=39歲,小軍的年齡是13×1=13歲,所以應該是5年后。
舉例-2: 姐姐今年13歲,弟弟今年9歲,當姐弟倆歲數的和是40歲時,兩人各應該是多少歲?
歲差不會變,今年的歲數差13-9=4幾年后也不會改變。
幾年后歲數和是40,歲數差是4,轉化為和差問題。則幾年后,姐姐的歲數:(40+4)÷2=22,弟弟的歲數:(40-4)÷2=18,所以答案是9年后。
14
余數問題
【口訣】:
余數有(N-1)個,最小的是1,最大的是(N-1)。
周期性變化時,不要看商,只要看余。
舉例: 如果時鐘現在表示的時間是18點整,那么分針旋轉1990圈后是幾點鐘?
分針旋轉一圈是1小時,旋轉24圈就是時針轉1圈,也就是時針回到原位。1980÷24的余數是22,所以相當于分針向前旋轉22個圈,分針向前旋轉22個圈相當于時針向前走22個小時,時針向前走22小時,也相當于向后24-22=2個小時,即相當于時針向后拔了2小時。即時針相當于是18-2=16(點)
end
聲明:本文內容來源于網絡,轉載請聯系原出處。封面圖片來自邑石網。奧數網尊重版權,如有侵權問題,請及時與管理員聯系處理。
大家都在玩的社團☞心情谁人懂☜加入社團和大家一起交流
